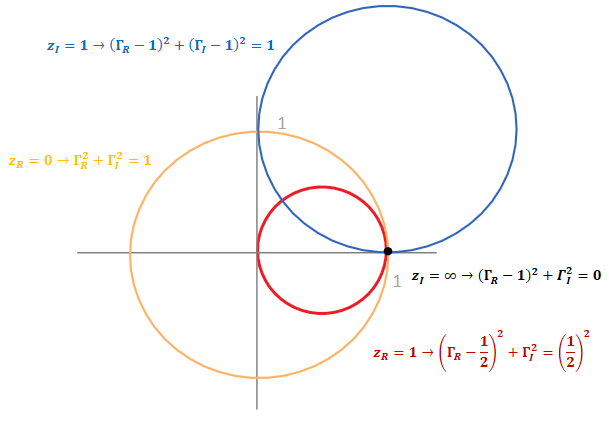Smith chart is used be mysterious to me. My daughter has an interesting book named my heart is like a zoo. This makes me come up with the story – my circle is like a Smith chart.

I can find lots of reference on Smith chart online, among which one of the most useful one is explained by Prof. F. Delssperger and he also develops a handy software to help us with matching and etc. After reading his slides, I kind of understand that Smith chart is trying to combine the impedance in Z plane with the reflection coefficient in Polar diagram. However, I am still confused about the exact size and position of the circles until I happen to find this derivation.

I extract the main flow of derivations here. For details, please click the above link.

First, the reflection coefficient is a complex number.

Second, this coefficient corresponds directly to a specific impedance as seen at the point it is measured. It can be calculated based on a load impedance Z_L (using a reference impedance Z₀). And the load impedance is further normalized to the reference impedance z_L=Z_L/Z₀.

Third, the normalized load impedance, which is also a complex number, can be expressed by the reflection coefficient.

Fourth, after rationalizing, the normalized load resistance z_R and load reactance z_I can be expressed by the following two circle equations.

Finally, thanks to the author’s derivation, the equations of the two circle can be rewritten in a familiar format.

For normalized load resistance:

For normalized load reactance:

Now we can draw some circles on Smith chart.