Is it possible to tell the stability of a negative-feedback circuit by just looking at its step response? The answer is yes. In this post, I will try to find the relationship between phase margin and ringing in step response.

I will start from the frequency domain and play with the equations we are familiar with. To simplify the problem, I assume it’s a unity negative-feedback second-order system. Denoting the DC gain by A, the two poles by f1 and f2, the unity-gain bandwidth by GBW (=Af1), the open-loop gain can be written as

.

The closed-loop gain can be thereafter written as

.

Express the denominator in the familiar control theory form, , where ξ is the damping factor and f_n the natural frequency.

     and   

If we take a close look at the damping factor, which tells the relative position between the second pole and the unity loop gain bandwidth, we shall know the phase margin as has been discussed in one of my old posts.

The peaking in the amplitude response can be found at  with a value equal to

.

Fig.1 Peaking in amplitude response

Now we have derived the relationship between phase margin and peaking in amplitude response. Let’s continue to look at the time domain. Considering we normally care about the underdamped case (ξ<1), the equation of its step response can be written as (detailed explanation and derivation can be referred to this link)

.

The peaking in the step response can be found at  with a value equal to

.

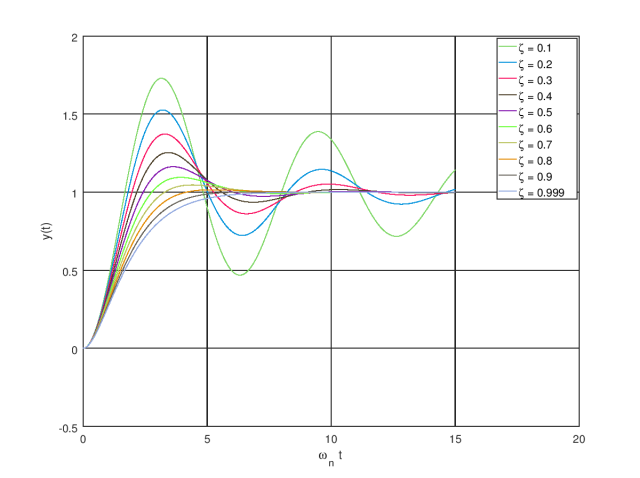
Fig.2 Ringing in step response

The exact number of the phase margin and peakings can now be easily calculated. Poor phase margin corresponds  to peaking in the frequency domain and ringing in the time domain.

Fig.3 Relationship between ξ , PM, Pf, and Pt